
Having now come to almost the end of the seasonal commitments in the community, it seemed time to pop up with a final post or two before we shut down for the holiday season. While we continue to fundraise, or otherwise source a chamber for use in the community, know that much behind the scenes work is continuing.
Today, an excerpt from the training and resource manual adds to the previous article DIVING PHYSICS, THE TRAINING & OPERATIONS MANUAL, FIFO SERVICES AND … PANTOMIME?. I hope to complete the manual early in 2020 and then decide what to do with it. The original idea was to limit its use to internal training and for use as a resource manual, but it occured to me it may be of benefit to other charitable operations. With this in mind we are considering having it peer reviewed and made available to others. One big advantage is that it has a significant section on legislation, written for the UK, but still a good guide for elsewhere in the world, which many could do with more information on.
Not everyone becomes instantly overjoyed though when a charity unit opens, and it is in the interests of various other business models to shush us and nip us in the bud. The health and safety legislation and practice section details which laws, and more importantly which amendments allow type 3 HBOT services to operate as complementary therapy services without medical oversight in the UK.
Today’s excerpt however, comes in the form of some further physics and gas laws. Specifically Dalton’s Law of Partial Pressures. It continues from our last physics discussion involving Henry’s Law. These two laws work very closely together and are the basis of decompression theory and gas solubility in liquid and detail how gas, for us this is oxygen, for divers it can be any inert gas, dissolves in and out of blood and tissues.
Described by physicist John Dalton in the early 1800’s, Dalton hails from Eaglesfield Cumbria, known at the time as Cumberland. Rather a significant connection considering his law describes one of the key mechanisms behind hyperbaric oxygen therapy. Ironic that Cumbria currently has no hyperbaric chamber.

Dalton’s Law or Dalton’s Law of Partial Pressures
Another of the gas laws, and likely most relevant of the three main gas laws in diving physics and medicine, is Dalton’s Law of Partial Pressure which works hand in hand with Henry’s Law previously discussed.
In chemistry and physics, Dalton’s Law (also called Dalton’s Law of Partial Pressures) states that in a mixture of non-reacting gases, the total pressure exerted is equal to the sum of the partial pressures of the individual gases.
It can be expressed mathematically as:
pTotal = p1+p2+p3…+pN
Where: pTotal is the total pressure of the gas and p1, p2 and pN represent the component gases in the mix. (pN being any number of additional gasses).
“Non-reactive” gases refer to interaction between gases while in the mix, and not to metabolic activity. For example, the oxygen and nitrogen in air do not react with each in the gas phase or gas mix.
As mentioned above, when discussing Henry’s Law, these two laws go hand in hand, they facilitate gas exchange in the lungs which will be discussed in more detail under physiology. These two laws are the hidden machinery behind HBOT and hyperbaric oxygen therapy. In fact, they are the gas laws behind human respiration. We are able to respire (breathe) because of these 2 laws and how they work together. They detail the mechanical function which takes place during pulmonary gas exchange where pressure differentials exist. For more on blood gas tensions see https://en.wikipedia.org/wiki/Blood_gas_tension
This law describes that, whether a gas is pure, or a gas is made up of different components, i.e. a mix, the portions or fractions of that gas (FG), will exert their relative proportionate amount of pressure in that gas, in the gas phase. As we mentioned, air exerts pressure. That is, air as a gas, exerts pressure equal to the surrounding pressure. This is called the pressure of the gas (PG). The pressure of any gas in a mix, for example nitrogen in air, is determined by its fraction in that gas or its percentage. It can be calculated by multiplying the fraction of that gas in the mix by the ambient pressure.
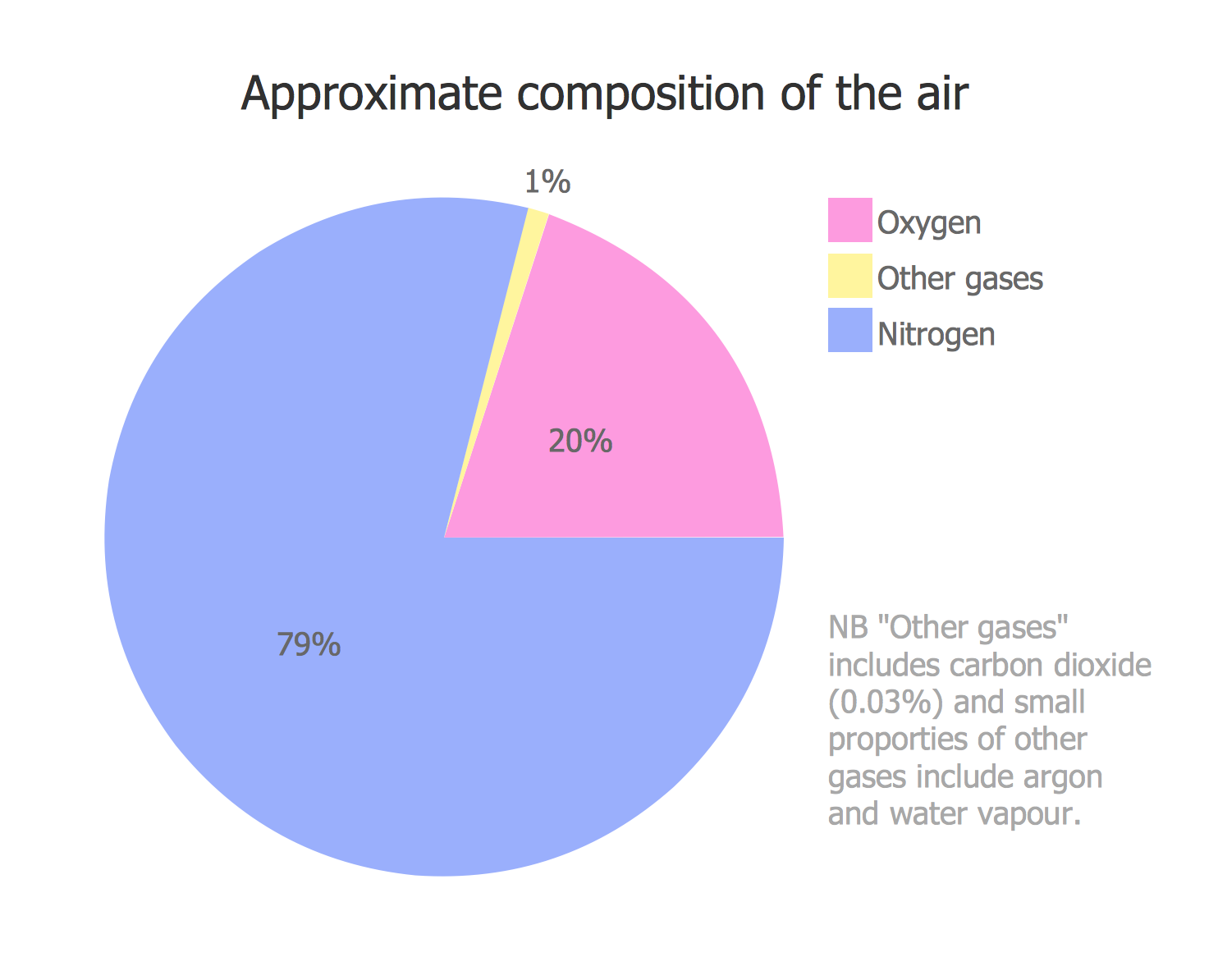
For example, in the case of pure oxygen at atmospheric pressure, or barometric pressure, the pressure of the gas is 1 atmosphere Absolute (1 ATA), (1×1=1), and if we had pure oxygen at an ambient pressure of 2 ATA, the pressure of that gas would be 2 ATA and so on (2 ATA x 1,0 fraction of gas (fg) = 2). Because it is a free gas not contained in any form of independent container but rather within a system such as the atmosphere itself, or chamber atmosphere, it exerts a pressure equal to the ambient pressure of the atmosphere it is in (ambient / surrounding pressure), either the actual atmosphere or artificial atmosphere such as that inside a chamber. This is the total pressure of the gas. For gases made up of component gases, each gas would exert a pressure directly proportional to its share or portion of that gas, or as described above, their fraction of that gas (FG). In the case of air, which we all understand readily, we have a gas mix of the following component constituents:

For the purposes of this instruction we will deal with the nitrogen and oxygen components in air. Carbon dioxide is entered at 400 parts per million and this fluctuates between 400, 416 and 420 parts per million depending on what information source is chosen. These differences are statistically and mathematically insignificant and as a rule of thumb in diving, we consider 400 ppm the current concentration in atmospheric air. It is worth mentioning though that gasses such as methane, carbon dioxide and carbon monoxide, among others, constitute contaminant gasses and have limits on their concentration in breathing air or chamber atmospheres. Sometimes these limits are expressed in partial pressures and this method can be used to calculate such.
Commonly in diving we refer to air as a mix of 21% oxygen, 78% nitrogen and 1% trace gases. The greatest trace gas being metabolically inert Argon. To further simplify this in terms of diving, we dismiss the trace gases as insignificant at the pressures commonly experienced in most diving, and we simply refer to air as 21/79. That is 21% oxygen (O2) and 79% nitrogen (N2). Or as some might even say 21/79 Nitrox. Nitrox being a mix of nitrogen and oxygen. Although we seldom refer to air as nitrox, but commonly refer to Nitrox as “Enriched Air” or “Enriched Air Nitrox”. The Acronym EANx is commonly used in diving.

Trace gas is dismissed because at current concentrations they present insignificant amounts of gas, that even under increased pressure, which is akin to increasing concentration, have no measurable physiological effect.
Now that we have a gas mix (air), and know its component fractions, 21% O2 and 79% N2, we can express the fractions of the component gases as fractions of barometric pressure at sea level. Expressed as 0,21 of that one atmosphere absolute (ATA) for oxygen, and 0,79 ATA for nitrogen. We also add the denotation “pp” after the pressure to signify the representation of partial pressure. Carbon Dioxide for example would have a partial pressure of 0.04 atmospheres absolute because its fraction in the gas in 0.04%.
Before we can determine a gas’s partial pressure, we must know how to first calculate the ambient pressure. Ambient pressure meaning the total or absolute pressure around us. This is easily calculated by adding 1 atmosphere to either chamber air pressure or diving water pressure. At sea level, not in a chamber, it is simply 1 atmosphere and it would be absolute. When diving 10 meters under the water, 1 additional atmosphere is encountered. Added to the 1 atmosphere above equals 2 atmospheres absolute and so on. 20 meters = 3 atmospheres absolute, 30 meters = 4 atmospheres absolute etc.
Expressed as follows:
To determine absolute pressure (ambient pressure), add atmospheric pressure to gage pressure or water pressure.
10 meters water (1 atm. water pressure) depth + 1 am atmosphere = 2 atm. absolute (ATA).
Some chambers will have gauges that measure in absolute pressure or even depth, and others will have gauges that measure in gauge pressure which exclude the additional atmosphere. For high pressure diving cylinders, it is inconsequential but not so for pressure measurement in a hyperbaric chamber. It is important to recognise and identify which gauges are installed on a chamber. It is important to become conversant in all measures, and easily able to recognise them and be able to convert values quickly and even be able to work simultaneously in different systems of measurement. Some protocols refer to depth, some to ATA and then some to just the amount of additional pressure added (gauge pressure). Understanding the concepts and expressions of pressure is paramount.

Partial pressure can now be calculated as follows:
To determine the partial pressure (PP) of a gas in a mix of gasses, multiply its fraction by the ambient pressure.
21% oxygen (Decimal 0,21) X 1 atmosphere absolute (ATA sea level) = 0,21 ATA partial pressure oxygen (ppO2).
79% nitrogen (Decimal 0,79) X 1 Atmosphere absolute (ATA sea level) = 0,79 ATA partial pressure nitrogen (ppN2).
And that’s the sum of it. Calculating partial pressures and fractions of a gas. The same equation can be reversed to calculate the fraction if the partial pressure is known.
If we doubled the ambient pressure by stepping into a pressure chamber and pressurising that chamber to the equivalent of 10 meters depth of sea water, (or indeed dived 10 meters under the water), we would be at 2 atmospheres absolute pressure as previously explained. Herewith calculated in the following example:
21% oxygen (Decimal 0,21) X 2 atmosphere absolute (ATA) = 0,42 ATA partial pressure oxygen (ppO2).
79% nitrogen (Decimal 0,79) X 2 Atmosphere absolute (ATA) = 1,58 ATA partial pressure nitrogen (ppN2).
One final example with odd numbers as follows:
To determine the partial pressure of oxygen and nitrogen in normal air at a depth of 27 meters of sea water calculated as follows:
First determine ambient pressure:
27 meters of depth = 2,7atm water pressure + 1 atm. atmospheric pressure = 3,7 ATA (atmospheres absolute)
For oxygen:
0,21 (FG) X 3.7 ATA = 0,777 ATA ppO2 (atmospheres absolute partial pressure oxygen).
For nitrogen:
0,79 (FG) X 3,7 ATA = 2,923 ATA ppN2 (atmospheres absolute partial pressure nitrogen).
It is important to understand these gas laws to some degree, in order to understand the concept of gas exchange in the lungs, also called gaseous interchange. Basically, it is the process by which the gases in the air we breathe enter the bloodstream, and as a knock-on effect, enter the individual tissues of the body, and then proceed on to enter each and every cell in those systems. This process is driven by pressure, and can be analysed by analysing partial pressures of the gasses we breathe. This explains oxygen transport, inert gas saturation and indeed any gas poisoning we may encounter, including pollution related poisoning. It also explains breathing, and these calculations are used across a wide spectrum of industries including but not limited to diving, aerospace, aviation, mountaineering, space exploration, anaesthetics and so on.
Contaminant concentration in breathing air is extremely important in hyperbarics and diving. As pressure increases, as shown above, so does the partial pressure and by extension it solubility in the blood. Breathing a contaminant gas at a given concentration, at twice atmospheric pressure is the same as doubling it’s concentration at normal pressure. This is so because increasing the fraction of the gas while pressure remains unchanged increases the partial pressure as shown above. This means that when pressure is increased for a diver or chamber occupant, the concentration of contaminant gases essentially increases as well, and what may not be particularly toxic at surface pressure could well become so under pressure.
Note:
Certain gasses such as oxygen can behave like a toxin at higher partial pressures and it is important to know how to calculate these in order to stay within prescribed limits of exposure. Oxygen toxicity is discussed in our three part series beginning with OXYGEN TOLERANCE – MYTH VS FACT – AN INTRODUCTION TO A THREE PART SERIES .
We aim to follow up with the third main gas law, Boyle’s Law soon. Boyle’s Law details the effects pressure has on the volume of a gas.
Until then, stay well and chat soon.
©Hayden Dunstan



4 thoughts on “Physics, John Dalton and The Cumbrian Connection”